

Spektralanalyse |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Der FarbindexDer Farbindex ist eine fundamentale Größe der modernen Astrophysik. Es handelt sich um die Helligkeitsdifferenz, die ein Stern in zwei verschiedenen Wellenlängenbereichen aufweist. Solche Farbindices können anhand der verschiedenen Bereiche des sichtbaren Lichts, aber auch des infraroten bzw. ultravioletten Bereichs gebildet werden. |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
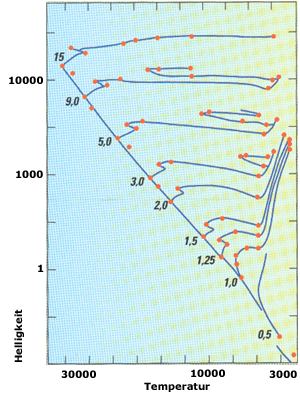
| Die Sternentwicklung nach dem Hauptreihenstadium. Ein Stern von der Masse der Sonne nimmt die Position 1,0 ein. Je größer die Masse, umso größer die Helligkeit, sodass die betreffenden Sterne immer höher im Diagramm angesiedelt sind. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
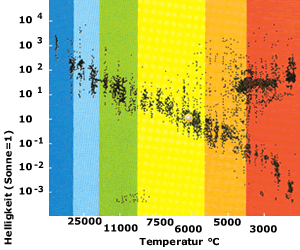
Das Hertzsprung Russel DiagrammDas Hertzsprung-Russel-Diagramm ist ein überaus nützliches Hilfsmittel, mit dem sich Helligkeit und Temperatur (bzw. Farbe) der Sterne in Beziehung setzen lassen. Auf dem HRD ordnen sich die Sterne vorwiegend in drei Zonen an: der Hauptreihe, dem Riesenast sowie dem Gebiet der Weißen Zwerge. |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
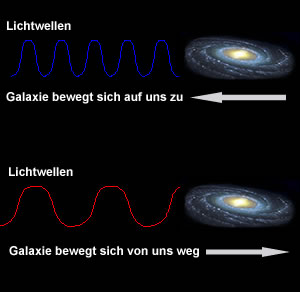
Dopplereffekt und RotverschiebungDas Phänomen des Dopplereffekts tritt auf, wenn ein Objekt, das eine elektromagnetische Welle aussendet, sich auf einen Beobachter zu oder weg bewegt. Das heißt, die elektromagnetische Welle wird dabei entweder gestaucht oder gedehnt. Um sich diesen Effekt besser vorstellen zu können, möchte ich folgendes Beispiel anführen: |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
RotverschiebungDie Rotverschiebung ergibt sich, wie bereits erwähnt, aus dem Phänomen des Dopplereffekts und muss grundsätzlich in drei einzelne Parameter untereilt werden. z (kosmologisch): Dieser Parameter ergibt sich aus der Tatsache, dass sich das Universum bzw. der Raum ausdehnt. Lichtwellen die den Raum durchwandern, werden dadurch in die Länge gezogen und erscheinen dem Beobachter auf der Erde rot- verschoben. Dieser Parameter ist ausschlaggebend für die Entfernungsbestimmung von Quasaren in sehr großen Distanzen. z (doppler): Dieser Wert gibt die Radialbewegung eines Objektes wieder, das noch nicht der Raumexpansion unterliegt. Darüber lässt sich beispielsweise bestimmen, ob sich eine Galaxie wie Andromeda auf uns zu- oder von uns weg bewegt. Grundsätzlich kann dieser Parameter zur Entfernungsbestimmung sehr weit entfernter Objekte, die der Raumexpansion unterliegen, vernachlässigt werden. z (grav): Hierbei handelt es sich um die gravitative Rotverschiebung. Diese konnte über das Doppelsternsystem Sirius A und Sirius B genau bestimmt werden. Sirius befindet sich 8,6 LJ von der Erde entfernt. Bei Sirius B handelt es sich um einen Weißen Zwerg der mit seinem Gravitationspotential, das 8000 mal über dem unserer Sonne liegt, Lichtstrahlen, die seine Oberfläche verlassen, maßgeblich beeinflusst. Ausschlaggebend dafür ist die Zeitdilation, die sich aus der Allgemeinen Relativitätstheorie ergibt. Zusammenfassend ergibt sich also die Rotverschiebung aus: z = z(kosmologisch) + z(grav) + z(doppler) wobei diese drei Parameter spektroskopisch nicht unterschieden werden können, sondern sich lediglich ihr prozentueller Anteil bestimmen lässt. |
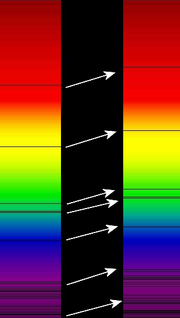 in dieser Darstellung wird die Spektralverschiebung eines weit entfernten Quasars (rechts) der unserer Sonne (links) gegenübergestellt. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
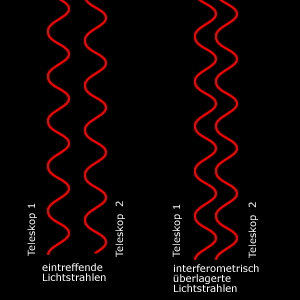
Interferometrie und Adaptive OptikEin grundsätzliches Problem für erdgebundene Teleskope, im Gegensatz zu Teleskopen im Weltraum, ist die Lichtbrechung, die durch unsere Atmosphäre verursacht wird. Um diesen Effekt möglichst zu reduzieren, werden heutige Großteleskope wie beispielsweise das VLT zum einem an Orten errichtet, die möglichst frei von atmospärischen Störungen sind und zum anderen werden sie mit sehr aufwändigen Technologien ausgestatten, um eine möglichst große und störungsfreie Lichtausbeute zu ermöglichen. Um atmosphärische Störungen auszugleichen, rüstet man heutige Teleskope mit sogenannter Adaptiver Optik aus. Dabei gibt es zwei verschiedene Möglichkeiten: Zum heutigen Stand der Technik lassen sich Parabolspiegel bis zu einem Durchmesser von maximal 8,4 Metern (LBT) aus einem Stück fertigen, da sie ansonsten zu schwer werden. Bei diesen Spiegeln bedient man sich einer sogenannten Regelelektronik, die im Strahlengang nach dem Hauptspiegel montiert ist. Ein weiterer großer Schritt in der Entwicklung erdgebundener Teleskope, war die Zusammenschaltung mehrerer Einzelteleskope zu einem einzigen großen Teleskop. Um dies zu ermöglichen, wird der Strahlengang jedes einzelnen Teleskopes in sogenannten Delay Lines geleitet, welche die unterschiedlichen Lauflängen des empfangenen Lichts synchronisieren (siehe Abb. rechts). Diese Methode nennt sich Interferometrie (siehe Abb. rechts). Die unterschiedliche Laufzeitdifferenz des Lichts ergibt sich zum einen aus den unterschiedlichen Standorten der Teleskope und zum anderen durch die scheinbare Bewegung eines beobachteten Objektes am Himmel, sofern es sich nicht im Zenit befindet. Dabei erreicht man eine Winkelauflösung, die der Summe der Spiegelfläche aller Einzelteleskope entspricht. Das VLT erreicht dabei beispielsweise bei der Beobachtung des Mondes eine Auflösung von 10 Metern. Das heisst, ein Bildpixel der CCD-Kamera entspricht dabei einem Durchmesser von 10 Metern auf ca. 380.000 km Distanz. |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Elektromagnetisches Spektrum |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Spektralklassen:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
- Startseite - Kontakt - Register - |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||